Question 11

Which of the following is not the graph of a quadratic polynomial?

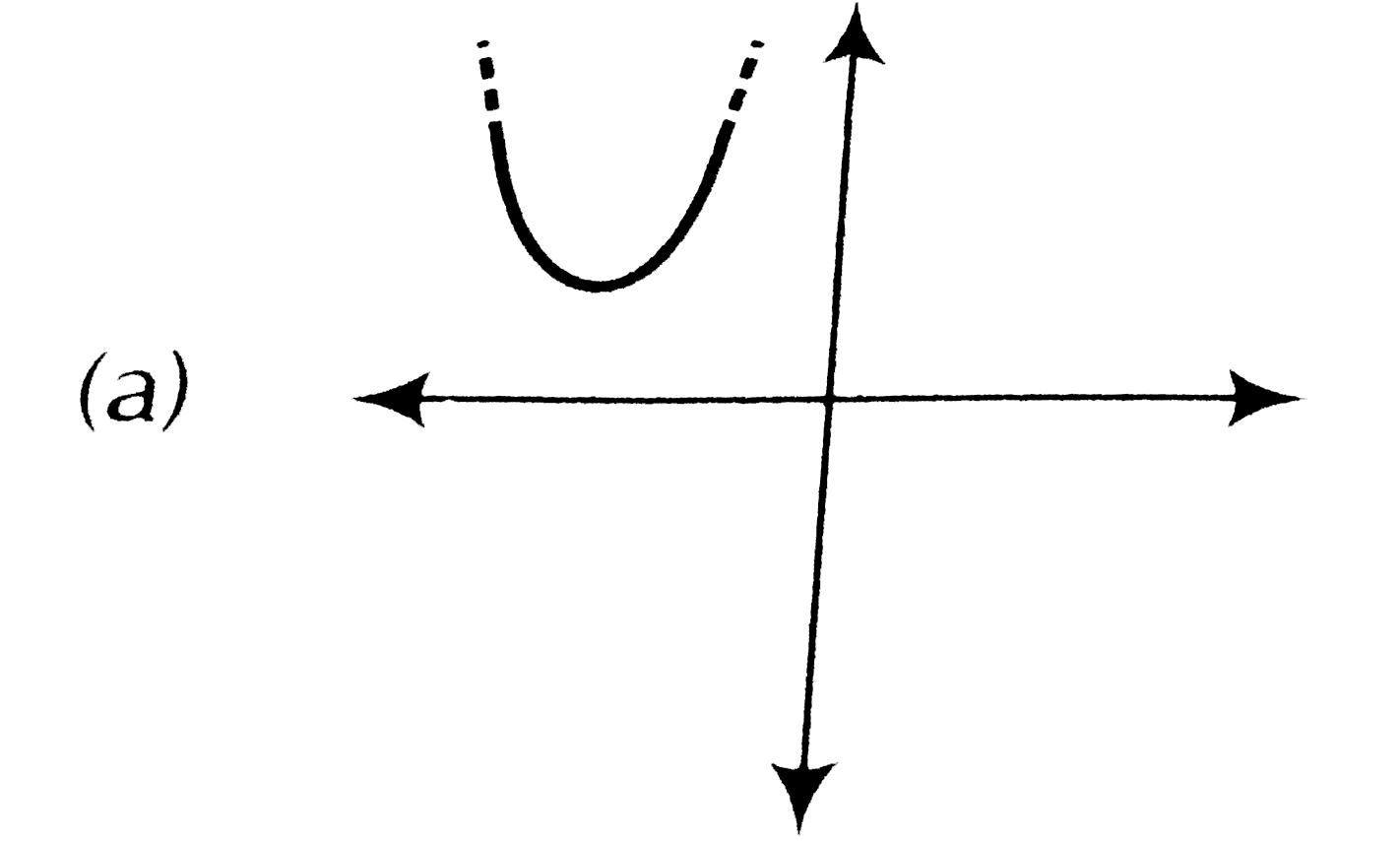
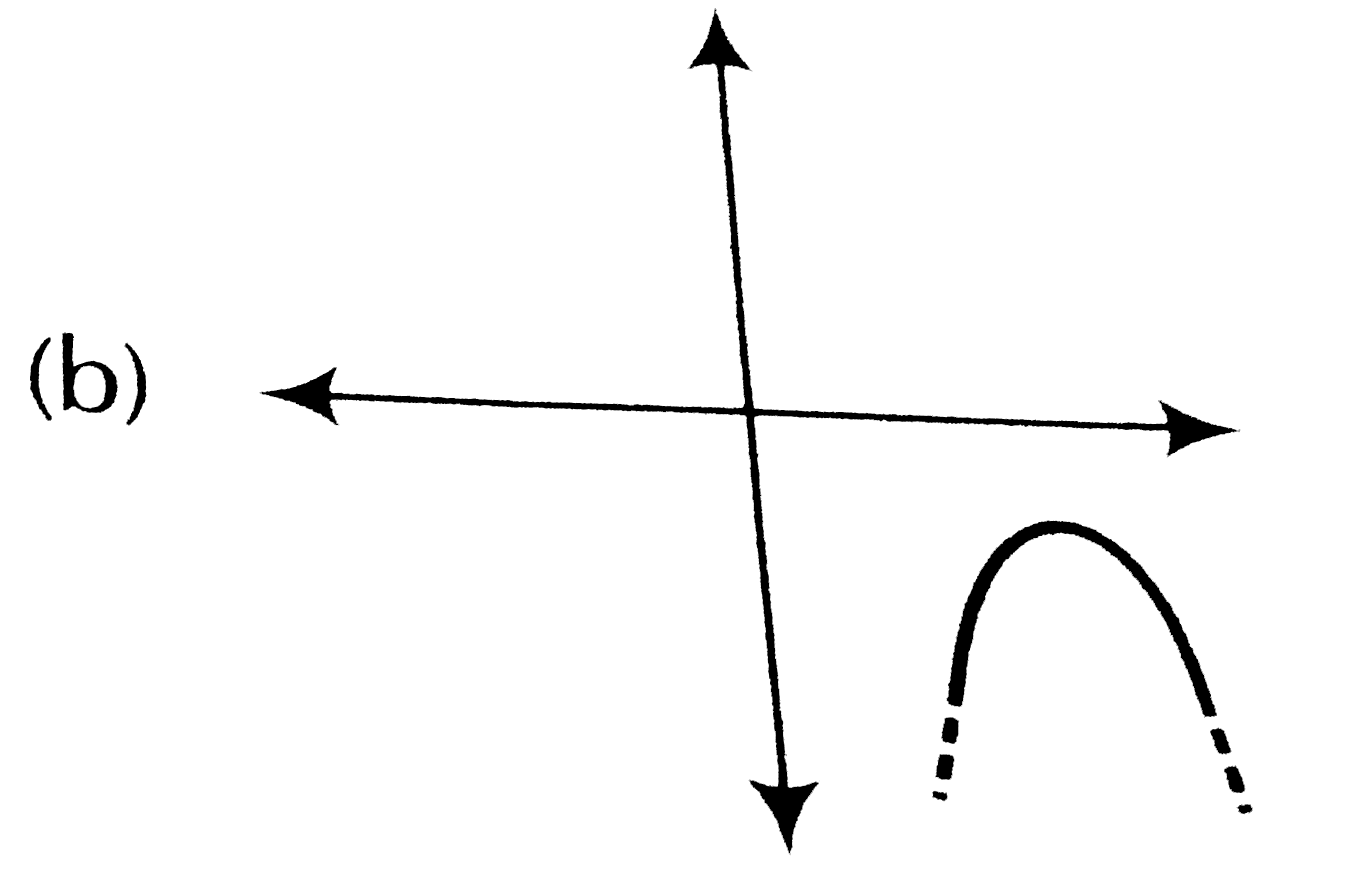
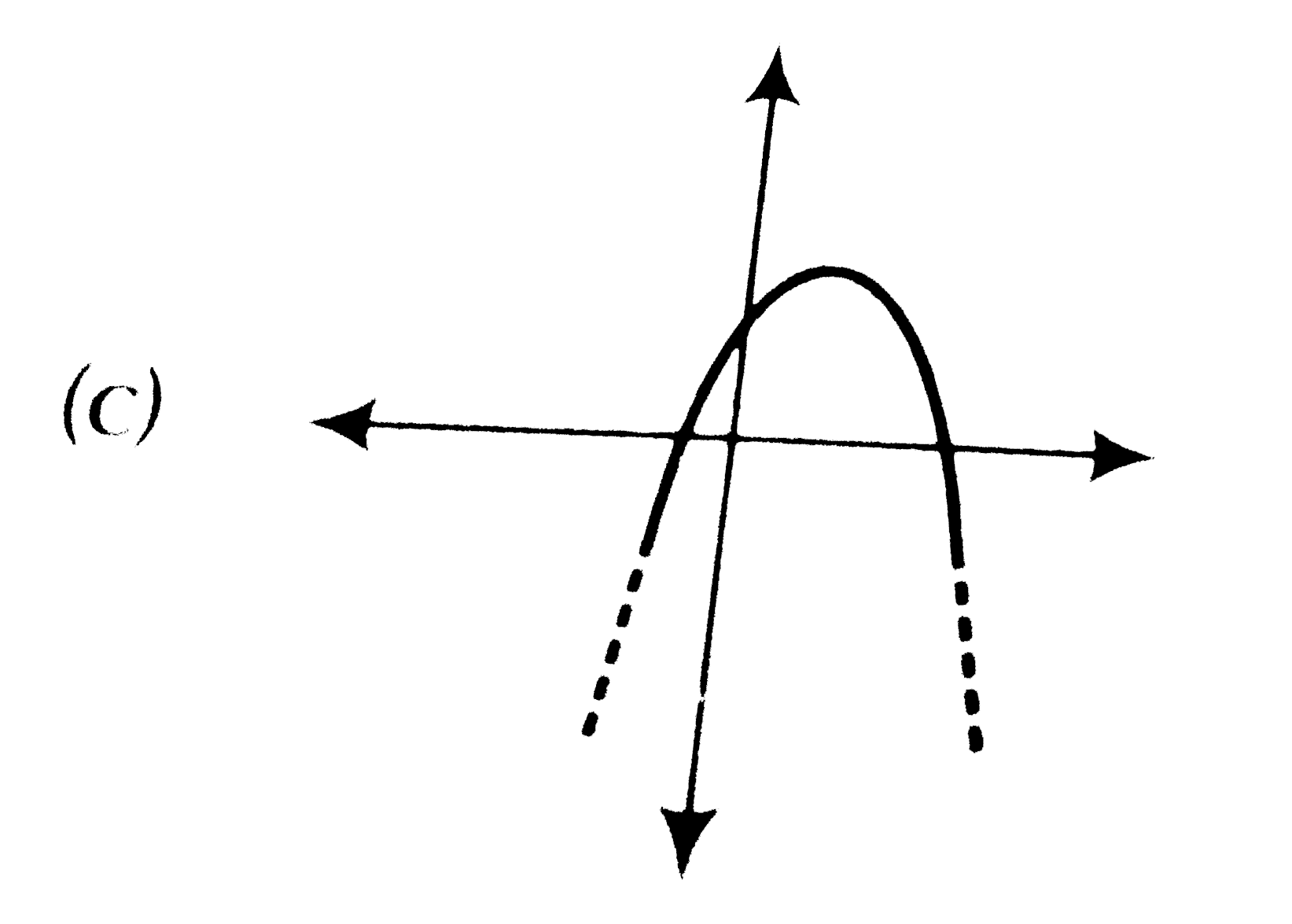
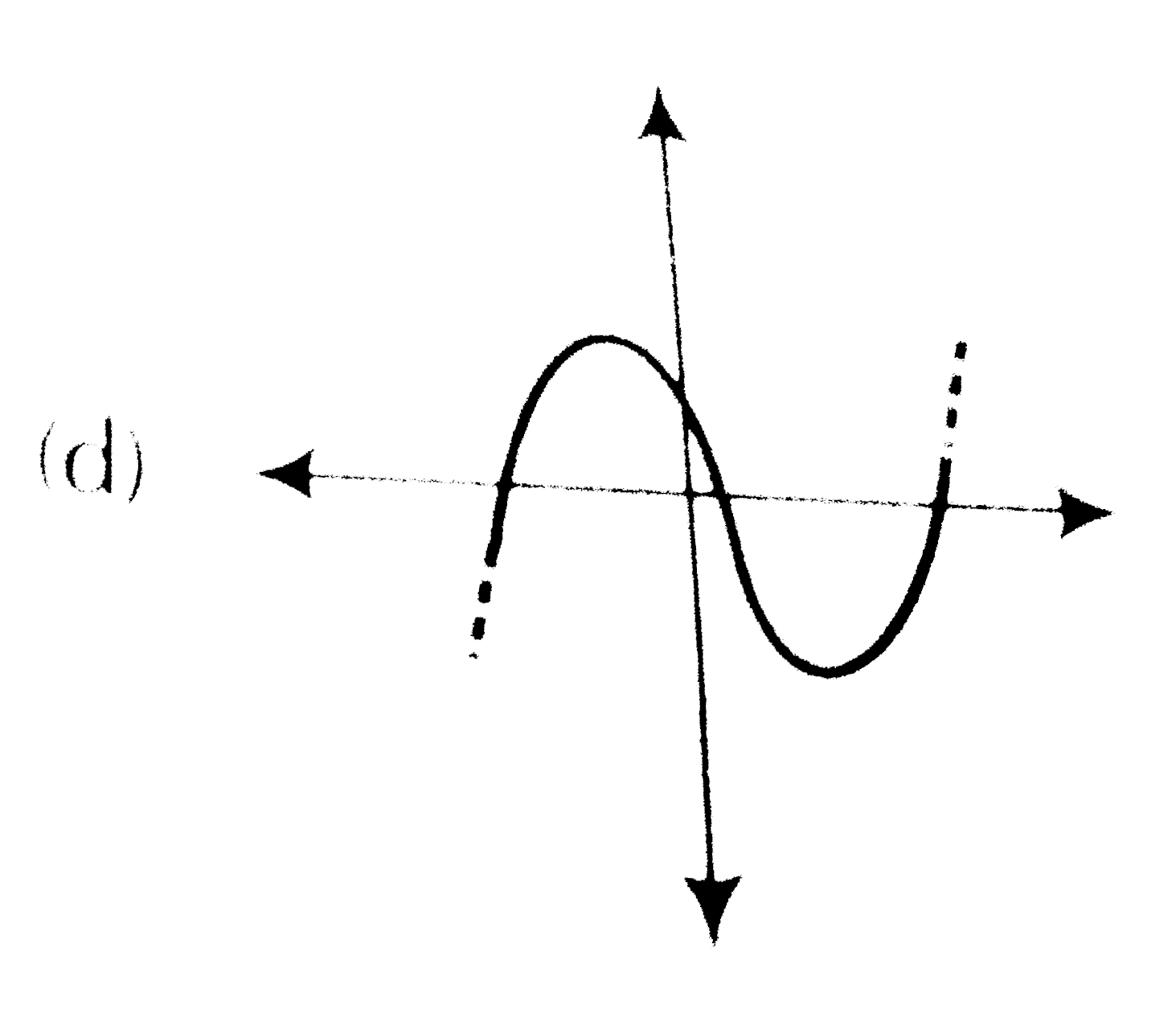
Solution:

To determine which of the given graphs is not the graph of a quadratic polynomial, we need to understand the characteristics of quadratic polynomials and their graphs.

1. Understanding Quadratic Polynomials:
A quadratic polynomial is generally expressed in the form $$a{x}^2+bx+c$$, where $$a,b,$$ and $$c$$ are constants and $$a\ne 0$$. The graph of a quadratic polynomial is a parabola.

Hint: Remember that the standard form of a quadratic polynomial is $$a{\mathrm{x2}}^{}+bx+c$$.

2. Roots of Quadratic Polynomials:
A quadratic polynomial can have at most 2 real roots. This means that the graph can intersect the x-axis at either 0, 1, or 2 points.

Hint: Consider the maximum number of intersections a parabola can have with the x-axis.

3. Shape of the Graph:
The graph of a quadratic polynomial can open upwards or downwards, depending on the sign of the coefficient $$a$$:
– If $$a>0$$, the parabola opens upwards.
– If $$a<0$$, the parabola opens downwards.

Hint: Check the direction of the parabola to determine the sign of $$a$$.

4. Analyzing the Given Graphs:
– Graph 1: This graph touches the x-axis at two points (two equal roots). This is a valid quadratic polynomial.
– Graph 2: This graph intersects the x-axis at two distinct points (two distinct roots). This is also a valid quadratic polynomial.
– Graph 3: This graph intersects the x-axis at three points. Since a quadratic polynomial cannot have more than 2 real roots, this graph cannot represent a quadratic polynomial.

Hint: Count the number of points where each graph intersects the x-axis.

5. Conclusion:
Based on the analysis, the graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.

Final Answer:
The graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.